The following is a conceptual description of the k.ba.fn.closest_point(mesh, pos) function.

refer to :
https://wizardmania.tistory.com/m/20
https://m.blog.naver.com/qio910/221778224660
https://forums.cgsociety.org/t/snap-vertices-to-nearest-point-on-curve-or-edge/1833911

Based on the links, the meaning of the function was conceptualized as an image.

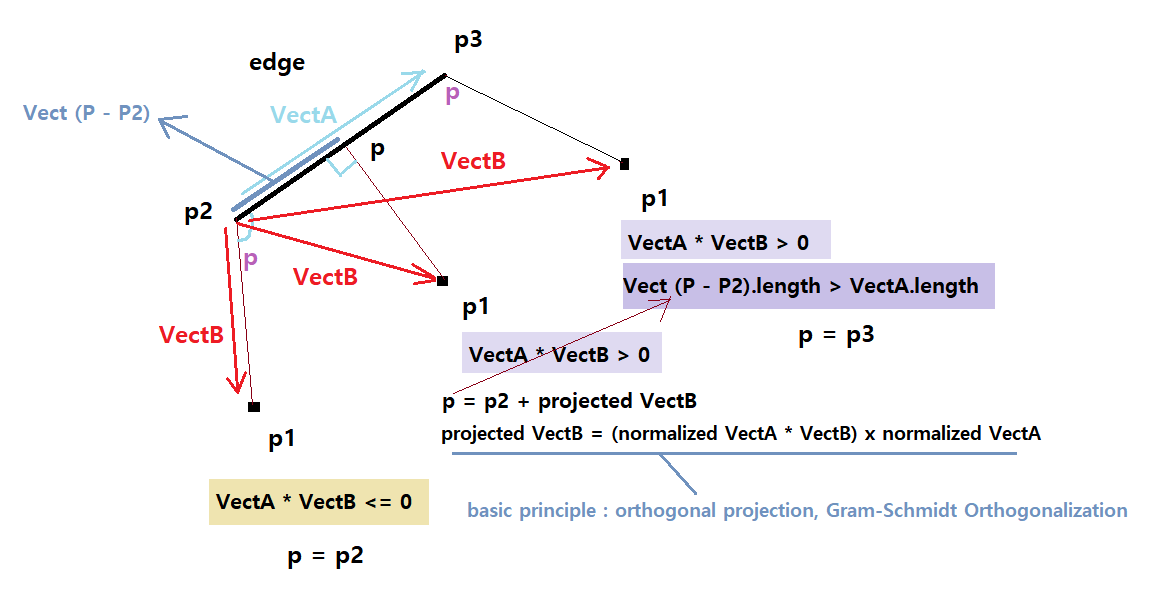
p1이 3가지 상황에 따라 p점(선분p2-p3와 점 p1의 교차점)을 구한다.

선분(Edge) 시작점에서 끝점을 향하는 벡터A와
선분 시작점에서 p1 지점을 향하는 벡터B의 내적이
0보다 적으면 두 벡터의 각은 둔각으로 p2 점쪽으로 p2 점을 벗어나 있는 경우이고
0보다 크면 두 벡터는 예각으로 선분 위에 있거나 p3 점쪽으로 p3 점을 벗어나 있는 경우이다.

다시 0보다 클때의 2가지 경우를 어떻게 분류하냐면
우선 선분상 P 지점을 Orthogonal Projection(정사영) 이라는 수학적 원리로 구한 후
p2에서 p의 거리가 에지 길이보다 크다면 p3를 벗어나 있는 경우라 판단할 수 있다.
반면 p1 점이 선분상에 놓여있지 않은 경우라면 p1에 각 끝 지점을 부여한다.

• 정사영 - VectorA에 투영된 VectB인 projected VectB는 수학적 공식으로 구한다
  projected VectB = (normalized VectA * VectB) x normalized VectA

• 실제로 직교하는 p1의 p계산은 p3를 벗어나는 p1의 p계산보다 먼저 이루어져야 한다
  실제로 직교하는 p1의 계산된 p를 가지고 조건을 판단해
  p3를 벗어나는 p1의 p계산을 오버라이드하기 때문이다.

• 내적은 교환법칙이 성립한다.